CH32X035以及CH32L103均支持USB PD功能,在将PD CC引脚作为普通IO使用时,在配置上有一些注意事项需要注意。
关于CH32X035 CC引脚使用注意事项:
CH32X035 CC引脚为PC14、PC15引脚,如下图:

在将CC引脚(PC14、PC15)作为普通IO配置成上拉时,若按照正常上拉配置,上拉电压大概2.2V左右。若想上拉电压达到正常供电电压3.3V,则需要进行如下配置,如下图:

注意要开启复用时钟,且需要对AFIO控制寄存器的位8置1,如下图:

CH32L103 CC引脚使用注意事项:
CH32L103 CC引脚为PB6、PB7引脚,如下图:
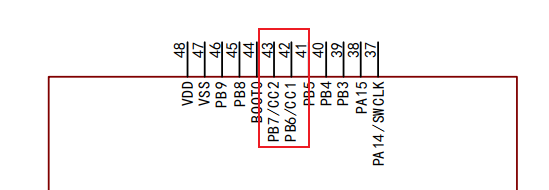
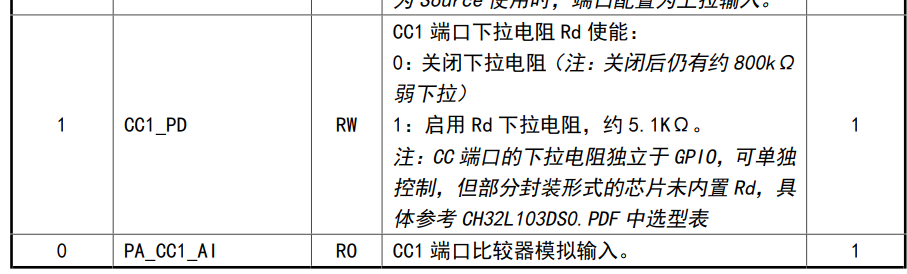
CH32L103部分型号MCU(如CH32L103K8U6、CH32L103F8U6)CC引脚内置下拉电阻Rd,且默认是开启的,在将CC引脚(PB6-CC1、PB7-CC2)作为普通IO使用时,注意要配置关闭下拉电阻,参考下图: